New tool reveals how the different shapes of organisms grow
A new tool has been created to explain how tissue growth leads to the range of plant and animal forms we see around us.
Developed by a team at the John Innes Centre, the new tool will be extremely useful for people trying to understand how 3D tissue shapes are generated.
Growth is fundamental to life. By understanding the principles of how tissues grow we can provide essential knowledge that can feed into many different applications, for example improving the shape of crops and organ regeneration.
Using the new tool, Dr Richard Kennaway and Prof Enrico Coen, from John Innes Centre, found a major difference between the growth of sheet tissues and bulk tissues.
Sheet tissue is thin in one direction but may be curved in space. Bulk tissue is thick in all three dimensions like an apple. It is much more constrained and less easily deformed.
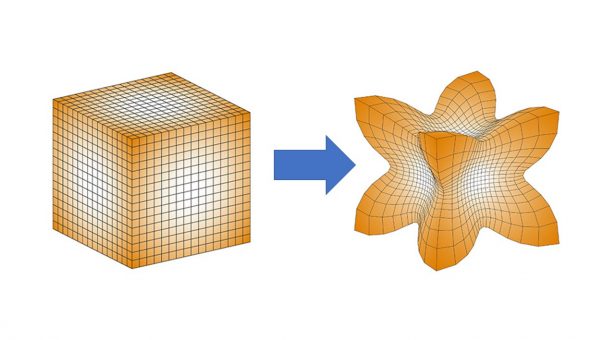
“It was difficult to predict the shapes you would get by intuition. For example, a cube with growth increasing out from the centre gave an unanticipated shape,” says Professor Enrico Coen.
Previous theories of growth start with a tissue sheet and have shown how they are deformed to create the shapes we see around us. This new framework is more general and shows how the tissue sheet itself is formed from a combination of a growth rate, that may vary in different regions of the tissue, and a single directionality, called a polarity field. Polarity fields are important for coordinating growth.
The findings of this study have led to the prediction that more directionality is needed to allow tissue sheets of varying lengths and widths to be formed. A second polarity field, at a right angle to the first, has been proposed.
Professor Coen reported “we were surprised how easily you could account for outgrowths and sheets using the new polarity field.” We can see the effects of this in nature with the vast range of leaf shapes.
The article appears in the journal Open Biology: ‘Volumetric finite-element modelling of biological growth‘